Estimating the view count distribution on TikTok
TikTok is unusual in that the views of video get are fairly unpredictable. Unlike other social media platforms like Facebook or Instagram, most views through TikTok are driven by a recommendation algorithm (rather than who you follow) so views can vary dramatically based on unpredictable nuances of the algorithm. Within the same week, I've had videos whose success differs by a factor of 10,000.
I want to get some sense of how likely my next video is to be successful. Merely looking at the average of my most recent videos is not very predictive, because of how random the view counts are. This post details a method for creating these predictions, as well as a calculator so that you can protect your own future success.
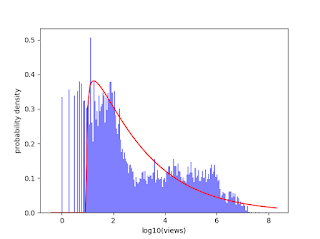
The view counts that videos get on TikTok are reasonably well approximated by a gamma distribution:
(Note that the x-axis is logged.)
This gives us a reasonable prior to use for a Bayesian update.
Recalling that the conjugate prior of a gamma distribution is a gamma distribution (i.e. it is self-conjugate), we can first create a gamma distribution over the parameter \(\beta\) of our gamma distribution as a prior, then add in the evidence from my view counts, resulting in a posterior distribution over \(\beta\).
(It's going to get very confusing that we are using a gamma distribution to estimate the parameters for a second gamma distribution. Through the rest of this, \(\alpha,\beta\) are the parameters for the distribution which estimates view counts, and \(\alpha_0,\beta_0\) are the hyperparameters for the distribution that estimates \(\beta\).)
1,000 samples of 200 videos each were created and a gamma distribution fit to each of them. I pulled out the parameter \(\beta\) from each distribution and made a histogram (blue rectangles), then fit a gamma distribution (orange line) to them.
Wikipedia tells us that if our prior is \(\Gamma(\beta; \alpha_0, \beta_0)\) then our posterior is $$\Gamma\left(\beta; \alpha + n\alpha_0, \beta_0+\sum_{i=0}^n x_i\right)$$ where \(n\) is the number of samples and \(x_i\) is the (logarithm) of the view count of sample \(i\).
Plugging this in, we can see how the posterior distribution of \(\beta\) based on my videos differs from the prior:
You can see that the posterior distribution is shifted the left, indicating a lower value of \(\beta\) (and hence a larger expected number of views, because I'm so popular):
The update from @charlidamelio is slightly larger:
Resulting in a very different probability distribution of her view count:
As the expected value of a gamma distribution is simply \(\frac{\alpha}{\beta}\), it's simple enough for us to calculate the expected values here:
Okay, so what does this all mean for you? You can estimate the expected number of views that your next video will create through the following steps:
I want to get some sense of how likely my next video is to be successful. Merely looking at the average of my most recent videos is not very predictive, because of how random the view counts are. This post details a method for creating these predictions, as well as a calculator so that you can protect your own future success.
Methodology
The view counts that videos get on TikTok are reasonably well approximated by a gamma distribution:
(Note that the x-axis is logged.)
This gives us a reasonable prior to use for a Bayesian update.
Recalling that the conjugate prior of a gamma distribution is a gamma distribution (i.e. it is self-conjugate), we can first create a gamma distribution over the parameter \(\beta\) of our gamma distribution as a prior, then add in the evidence from my view counts, resulting in a posterior distribution over \(\beta\).
(It's going to get very confusing that we are using a gamma distribution to estimate the parameters for a second gamma distribution. Through the rest of this, \(\alpha,\beta\) are the parameters for the distribution which estimates view counts, and \(\alpha_0,\beta_0\) are the hyperparameters for the distribution that estimates \(\beta\).)
1,000 samples of 200 videos each were created and a gamma distribution fit to each of them. I pulled out the parameter \(\beta\) from each distribution and made a histogram (blue rectangles), then fit a gamma distribution (orange line) to them.
Plugging this in, we can see how the posterior distribution of \(\beta\) based on my videos differs from the prior:
The update from @charlidamelio is slightly larger:
Resulting in a very different probability distribution of her view count:
As the expected value of a gamma distribution is simply \(\frac{\alpha}{\beta}\), it's simple enough for us to calculate the expected values here:
\(E[\beta]\)
|
\(E[\log(views)]\)
|
\(E[views]\)
|
|
Prior (average for the TikTok community)
|
0.647
|
2.197
|
157
|
Me
|
0.485
|
2.934
|
859
|
@charlidamelio
|
0.185
|
7.665
|
46,244,645
|
Calculation
Okay, so what does this all mean for you? You can estimate the expected number of views that your next video will create through the following steps:
- Calculate \(n\), the number of videos you've published, and \(s\), the total number of views those videos have received
- Calculate \(\alpha_0 = 53.865+ n\) and \(\beta_0 = 83.099 + s\)
- Calculate \(\beta =\alpha_0/\beta_0\)
- Calculate \(\log_{10}(views) = 1.42158 /\beta\)
- Calculate \(views =10^{\log_{10}(views)}\)
Or you can use the following form:
Research done in collaboration with @lilweehag






How does deleted videos impact this? It's so annoying how the draft button and publish button aren't more clearly color coded.
ReplyDeletePlease my sport
ReplyDeleteSince arbutin inhibits tyrosinase, an enzyme that helps with melanin production, it can prevent dark spots or even help fade them, leading to a more even complexion. https://www.cholley.com
ReplyDeleteFormation of the kinds of the designs are implied for the suggestions. Theme of the NewArabia for the turns. Change is held for the dynamic use for the official count for the argument for the website by all choices.
ReplyDeleteAn estimated review counter and parameter is piled for the approach for all offers. The tinge for the medium review is sorted by all customers. Part is played for the hunch for the alike features for the formation and guiles by all offers for the customers.
ReplyDeleteInteresting thoughtss
ReplyDeleteA pet portraits provides a wonderful way to keep beloved animals close, transforming a simple image into a work of art that highlights each pet’s character.
ReplyDeleteSmooth, fun, and rewarding! This Slot Gacor platform is perfect for anyone who loves online slots. The variety of games and quick payouts make it a great choice for both new and experienced players.
ReplyDeleteIt’s been a few weeks, and no matches on Tinder I’m starting to wonder why there are no matches on Hinge. I’ve tried changing my photos, updating my prompts, but it feels like nothing is working. If anyone has any tips on how to improve my profile, I’d love some advice!
ReplyDeleteTopanHoki Slot Gacor 2025 presents a wide selection of gacor games that are always ready to give you jackpots and other attractive prizes. topanhoki
ReplyDeletetpn77the real deal for trusted slot servers no cap
ReplyDeleteEstimating the distribution of views on TikTok (May 31, 2020) showcases the difference in user engagement for content. The analysis of such patterns informs algorithmic behavior. Research like this encourages new data science research topics , particularly within social media analytics, where trends, predictions, and modeling user behavior persist and bring new insights.
ReplyDeleteI highly recommend the ok win game to anyone who loves online gaming and real rewards. The platform offers smooth gameplay, fast withdrawals, and plenty of bonus opportunities. OK Win Game is reliable, entertaining, and easy to use. Whether you’re new or experienced, you’ll enjoy the exciting features, secure transactions, and the chance to win amazing prizes every day on OKWIN.
ReplyDelete